MARK EARL CASIDA

Professeur des universités (UGA)

SITh

Profile picture for user casidam

Coordonnées

Bâtiment : Chimie C

Bureau : 210

Mark.Casida@univ-grenoble-alpes.fr

Site web :

Last update: 12 November 2024

The references are by author initials and year (e.g. [MDC24] is for Magero, Darghouth, and Casida in 2024) and refer to my Publications.

EXPERTISE

I am a theoretical physical chemist/chemical physicist specializing in electronic structure theory (quantum chemistry).  I am particularly interested in the exploration of and the development of improved methods for treating difficult problems such as electronic excited states in transition metal complexes, organic and organometallic photochemistry, and molecules for molecular electronic materials.  My work often involves many-body perturbation theory (MBPT), density-functional theory, and mixed quantum/classical methods for photodynamics.

In some ways, my research interests and expertise are very interdisciplinary.  Thus I have served on PhD juries for students in both chemistry and physics departments and I have also served as an external examiner in both chemistry and physics.  Students who work with me are typically exposed to both areas.

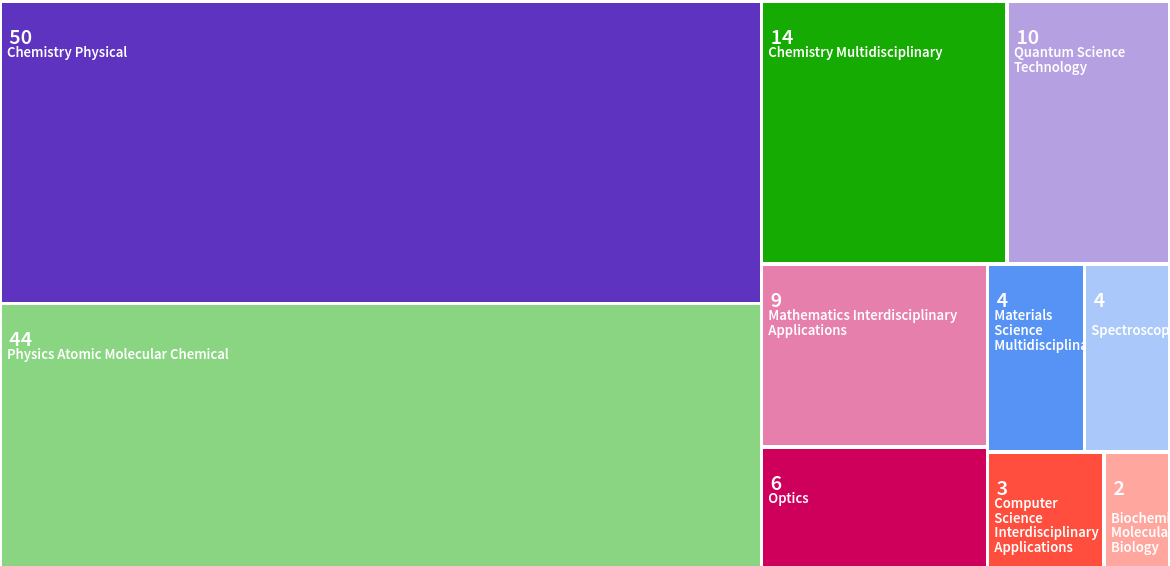
The Web of Science offers another perspective on the interdisciplinary nature of my work via the following diagram showing its classification of the areas of my various publications:

CURRENT RESEARCH INTERESTS

Nowadays, density-functional theory (DFT) is the work horse for most electronic structure calculations.  However we have noticed that DFT often fails for cases of strong correlation such as molecular configurations where bonds are being made or broken in the ground state.  This is also exactly where time-dependent (TD) DFT suffers from qualitatively incorrect descriptions of excited-state potential energy surfaces (PESs).  This is why I am now investigating multideterminantal (MDET) DFT methods.  The applications that I have in mind are generally to organic molecules and transition metal complexes in molecular electronic materials.

SOME RESEARCH ACCOMPLISHMENTS

I have contributed work on a number of interesting problems over the years.  As the list is long, I have provided a

TABLE OF CONTENTS

  • MULTIPLET SUM METHOD (MSM) DENSITY-FUNCTIONAL THEORY (DFT)
  • TIME-DEPENDENT DENSITY-FUNCTIONAL THEORY FOR PHOTOCHEMISTRY
  • TIME-DEPENDENT DENSITY-FUNCTIONAL THEORY FOR SPECTROSCOPY
  • LUMINESCENCE IN RUTHENIUM(II) POLYPYRIDINE COMPLEXES
  • MODELING KEY PHENOMENA IN ORGANIC SOLAR CELLS
  • DFT MODELING OF SPIN-CROSSOVER COMPOUNDS
  • NUCLEAR MAGNETIC RESONANCE (NMR) SHIELDINGS FROM DENSITY-FUNCTIONAL THEORY (DFT)
  • OPTIMIZED-EFFECTIVE POTENTIAL
  • MODELING ELECTRON MOMENTUM SPECTROSCOPY TRIPLE-DIFFERENTIAL CROSS-SECTIONS
  • SIMPLE GREEN FUNCTION SELF-ENERGY APPROXIMATIONS
 
MULTIPLET SUM METHOD (MSM) DENSITY-FUNCTIONAL THEORY (DFT)
 
Articles [PEMC21,PBEC23]
 

Electronic correlation was defined by Löwdin as the part of the electronic energy which cannot be captured by a single-determinantal Ansatz for the wave function [i.e., by the Hartree-Fock (HF) approximation].  This correlation is of three types: static, due to exact (symmetry-induced) degenerate states; nondynamic, due to quasidegenerate states; and dynamic, which is the type of correlation best described by (single-determinantal) density-funcational theory (DFT).  The historical method for treating static correlation in DFT is the MSM.

MSM-DFT was introduced by Ziegler, Rauk, and Baerends as a way to treat spin multiplets.  Daul extended MSM-DFT to transition metal complexes.  The basic idea of MSM-DFT is to solve a small configuration interaction (CI) problem where the elements of the CI matrix are reduced only to calculations involving single-determinant energies.  We recently showed how MSM-DFT may be applied to the important problem of singlet oxygen [PEMC21].

Current efforts are aimed at using diagrammatic analysis of CI elements to extend MSM-DFT to cases without symmetry and hence to include not just static correlation but also nondynamical correlation [PBEC23].

TIME-DEPENDENT DENSITY-FUNCTIONAL THEORY FOR PHOTOCHEMISTRY
 

Articles [CCS98,CJI+07,TTR+08,VFC15,DCZ+21]

Mixed quantum/classical Tully-type fewest switches surface hopping (FSSH) time-dependent (TD) density-functional theory (DFT) photodynamics simulations of photochemical reactions were one a dream and are now a reality.  In the beginning, we mapped out potential energy surfaces (PESs) along key pathways [CCS98,CJI+07,VFC15].  It became clear that TD-DFT could describe avoided crossings, that triplet instabilities and effective noninteracting v-representability can cause problems, some of which are very much attenuated, if not solved by the Tamm-Dancoff approximation (TDA).  Underestimates in charge transfer excitation energies were often used as an excuse to prefer complete active space self-consistent field (CASSCF) calculations to TD-DFT calculations in photobiology.  However recent work showed that, when properly used, TD-DFT can actually be more reliable than CASSCF in modeling the photochemistry of vision [VFC15].  We were also involved in some of the very earliest investigation of FSSH TD-DFT for photochemistry [TTR+08].  Since then, we have also used the FSSH method with the semi-empirical TD density-functional tight binding (DFTB) method to investigate charge transfer in photovoltaics [DCZ+21].  FSSH photodynamics is a fascinating area with its own challenges which is currently prospering and which is likely to see continued improvements in the near future.

TIME-DEPENDENT DENSITY-FUNCTIONAL THEORY FOR SPECTROSCOPY
 

Articles [CJB+94,C95b,JCS95,C96,CJC+98,CS00,C05,CIC06,C09,ICJC09,IFP+06,
HNI+10,HIRC11,NCGD11,CH12,NGC+12,CH15,MC17]

A quarter of a century ago, I developed the first practical molecular formulation of time-dependent density-functional theory (TDDFT) response theory [C95b], and we reported the first implementation of such a method [CJB+94].  It is similar to time-dependent Hartree-Fock (TDHF) but has the advantage that it includes correlation not present in TDHF, and enjoys the computational advantages of density-functional theory (DFT) as well. I have also extended the auxiliary-function techniques often used in Gaussian-orbital-based time-independent molecular DFT programs to the calculation of the coupling matrix [C95b,C96], thus allowing the costly four-center integrals to be replaced with three-center integrals. When appropriately implemented, this provides a method for calculating molecular electronic spectra which scales as O(N3) with the number of atoms [C96], an order of magnitude improvement over the least computationally demanding conventional ab initio methods for calculating these properties. Yet the results are remarkably good. The TDDFT results, within the simple local density approximation (i.e. TDLDA), for low-lying excitation energies are considerably better than those from TDHF or singles configuration interaction (CIS), and are more comparable to results from more expensive, correlated ab initio methods than to those of TDHF or CIS [JCS95,CJC+98]. My molecular formulation of TDDFT has been rapidly adopted and is now implemented in the major quantum chemistry packages that include DFT, worldwide. It is widely used and applications using the method include studies of the spectra of chlorophyll a, fullerenes, polyacetylenes, transition metal coordination compounds, and phototoxic drugs.

While my TDDFT method represents a great improvement over the previously available methods for calculating molecular excitation spectra, it is not without limitations. Most of the difficulties can be traced back to some aspect of the approximations used for the underlying exchange-correlation functional. Despite the success of the applications mentionned above (or perhaps because of this success!), there is a desire to continue improving TDDFT to extend its domain of applicability. Part of this is a matter of improving approximations for the exchange-correlation functional. (A review of exchange-correlation functionals for TDDFT up to 1996 is given in my article [C96].) The simplest functional, that is the time-dependent local density approximation (TDLDA), already often gives excellent results for lower excitation energies [JCS95,CJC+98]. However, we have demonstrated that the use of a functional whose exchange-correlation potential, vxc, has the correct (-1/r) asymptotic behavior is critical for the calculation of higher energy excitations [CJC+98]. In subsequent work [CCS98,CS00], we introduced an asymptotic correction (AC) to compensate for the fact that neither the LDA nor generalized gradient approximations (GGA's) possess the derivative discontinuity with respect to particle number which is characteristic of the exact functional [C99].  This AC leads to improvements in the higher excitation energies, and a similar correction has now been adopted by Tozer and Handy. The resulting ability to handle both valence and Rydberg states, and to describe their mixing, has permitted us to report the first avoided crossing due to nontrivial configuration mixing calculated by a first-principles DFT method [CCS98].

Major work on developing TD-DFT since that time has included its implementation in the wavelet-based program BigDFT [NCGD11,NGC+12], spin-flip TD-DFT and conical intersections [HNI+10], modifications needed for treating open-shell systems including the calculation spin contamination [CIC06,ICJC09,MC17], dressed TD-DFT [C05,HIRC11,CH15].  We have also contributed important reviews of TD-DFT of which the most recent are [C09,CH12].

LUMINESCENCE IN RUTHENIUM(II) POLYPYRIDINE COMPLEXES
 
Articles [WJL+14,MCA+17,MMAC22,MDC24]
 

Luminescent ruthenium(II) polypyridine complexes have long-lived triplet metal-ligand charge transfer (3MLCT) excited states which make them ideal candidates for use in photomolecular devices (PMDs) including, but not limited to, solar cells [MMAC22].  An  improved understanding of the luminescence mechanism can only help in PMD design.  We have been particularly interested in finding a ligand field theory (LFT) like way to characterize luminescence lifetimes based upon density-functional theory (DFT) calculations.  The first problem was to recover LFT from DFT.  This was accomplished in Ref. [WJL+14] using the partial density of states (PDOS) method.  We then sought, and found, an orbital-based luminescence index (LI3, for the third attempt at such a luminescence index) on the basis of comparison between our LFT-like energies and experimental luminescence lifetimes at room temperature and liquid nitrogen temperature for about one hundred complexes [MCA+17].  DFT exploration of the triplet potential energy surface (PES) for 3MLCT -> 3MC trans dissociation, showed that the gas-phase PES shows a complicated structure which includes a bifurcating pathway.  The excited-state reaction mechanism consists of a charge transfer to a single bipyridine ligand in the form of a symmetric transition state.  This reaction path from this transition state shows a bifurcation to one of two 3MC products.  As a result, LI3 does not correlate with the 3MLCT -> 3MC trans dissociation barrier height but rather with the  3MLCT-3MC energy difference [MDC24].

MODELING KEY PHENOMENA IN ORGANIC SOLAR CELLS
 
Articles [DCT+15,TCC17,DCJ+18,TCDA19,DCZ+21,MMA22,TANC23]
 

This work divides into two complementary approaches, one fundamental and the other very much applied.  In order to explore some of the fundamental physics of organic solar cells, we have turned to the density-functional tight binding (DFTB) method which is a semi-empirical approximation to density-functional theory (DFT).  We first evaluated DFTB for its ability to describe the ionization potentials and electron affinities of medium-sized molecules important for organic solar cells by comparison against experiment and high-quality GW Green's function calculations [DCT+15].  We then turned to time-dependent (TD) DFTB and TD-DFT calculations to investigate excitonic effects on absorption spectra when molecules interact in the condensed phase [DCJ+18].  This study revealed the surprising underestimation of TD-DFT(B) charge transfer excitation energies in a case where no net charge transfer occurs.  We also used mixed quantum/classical Tully-type fewest switches surface hopping (FSSH) range-separated TD-DFTB to investigate the dynamics of charge transfer between pentacene and buckminsterfullerene (i.e., C60) [DCZ+21].  Statistical averaging is needed over a large number of FSSH trajectories in order to obtain agreement with the original surface hopping model.  Previous FSSH TD-DFT work, though interesting, was limited to too few trajectories for good statistics.  In contrast, the efficiency of the semi-empirical method gave us the statistics missing in previous FSSH TD-DFT work and allowed us to see that an electron does not simply hop from pentacene to C60, but rather that the initial excitation localized on pentacene delocalizes over both molecules and then the charges relocalize to make the final electron transfer, similarly to the flickering polaron picture of conduction in organic semiconductors.

Other work may best be classified as applied physics aimed at optimizing the structure of organic molecules for use in organic solar cells.  As the whole area of organic solar cells is evolving extremely rapidly, we too have been forced to use increasingly sophisticated models to capture key phenomena.  The recent history of organic solar cells has been divided into three stages: (i) P3HT:PCBM solar cells, (ii) DON:PCBM solar cells, and now (iii) DON:NFA solar cells.  Here DON stands for a donor material other than the P3HT polymer and NFA stands for a nonfullerene acceptor material.  Our initial work [TCC+17,TCDA18,TZCA19] was based upon Scharber's model for estimated photoconversion efficiencies of DON:PCBM solar cells.  Our more recent work re-examines the validation of theoretical methods in this area introduces a new modified Scharber plot for estimating photoconversion efficiencies of DON:NFA solar cells [TANC23].

DFT MODELING OF SPIN-CROSSOVER COMPOUNDS
 
Articles [FMC+04,FCL+05,LVH+05,GBFC05,ZBF+07,LC22]
 

The relativethermodynamic stabilities of certain transition metal complexes is such that, by tuning the choice of ligand, the complexes may be switched between high- and low-spin states by a simple change in temperature. The ability to predict this transition temperature requires a very precise understanding of the inter and intramolecular energy and entropy contributions to the high-spin/low-spin free energy difference. It is already an excited-state problem. The situation becomes even more interesting, from the point of view of fabricating optical devices, for those complexes which also show a significant kinetic barrier between the ground low-spin state and the metastable high-spin state. It then becomes possible to create a molecular optical switch by laser-induced switching between the two states which have different magnetic properties, effective volumes, and colors. A correct modeling of the phenomenon requires the ability to calculate the relative energies of the two low-energy states and ultimately of the manifold of excited states, including numerous open-shell states. As such it is a great challenge for any first principles method, DFT or otherwise.

The development of a DFT-based protocal for describing spin-crossover in Fe(II) compounds was the subject of the thesis of Antony Fouqueau. It involved state-of-the-art ab initio calculations on two small clusters, [Fe(H2O)6]2+ and [Fe(NH3)6]2+, for comparison with a wide range of DFT calculations [FMC+04,FCL+05]. It also involved direct comparison with experimental information about the relative stabilities of the high- and low-spin states of [Fe(bpy)3]2+ and Fe(L)('NHS4')] [LVH+05,GBFC05]. In these complexes, Hartree-Fock over estimates spin-pairing energies, thereby tending to over stabilize the high-spin states. Prior to our work, it had been felt that DFT tended to under estimate spin-pairing energies, thereby artificially favoring low-spin states. One popular solution was Markus Reiher's reparameterization, B3LYP*, of the popular B3LYP hybrid functional. We were able to show that some modern generalized gradient approximations (GGAs) could do as well as or better than the B3LYP* functional for describing relative spin energetics, especially the RPBE and OLYP functionals. This is very good news for those who wish to model large spin crossover compounds since only GGAs can take advantage of plane wave or charge density fitting techniques. In a more recent joint article [ZBF+07], we have gone further and argued that, whereas the separation between potential energy surfaces between different spin states is very sensitive to the choice of functional, the shapes of potential energy surfaces are relatively insensitive to the choice of functional. This provides hope that much of the computational work on spin crossover complexes can be carried out using less expensive methods, with just a few more elaborate calculations being needed to fix the precise separation between potential energy surfaces. Articles [LVH+05,GBF+05,ZBF+07] discuss some of the factors which make some functionals better descriptors than others of spin pairing energies.  In 2022, Latévi M. Lawson Daku and I published a summary of our work in this area [LC22].

NUCLEAR MAGNETIC RESONANCE (NMR) SHIELDINGS FROM DENSITY-FUNCTIONAL THEORY (DFT)

Articles [MMCS94,FCS03a,FCS03b]

Since NMR is one of the most important spectroscopies for chemists, it would be nice to have an efficient way to calculate chemical shifts within DFT. Our now classic 1994 paper [MMCS94] proposes the Sum-Over-States Density-Functional Perturbation Theory (SOS-DFPT) method for doing just this. One unsatisfying aspect of that work was the somewhat ad hoc nature of the correction to the uncoupled approximation. More recently, we have shown how a precise form of this correction term (which we call "Loc.3") can be derived from time-dependent density-functional theory and performs as well as or better than the previous Loc.1 and Loc.2 approximations in SOS-DFPT [FCS03a,FCS03b].

OPTIMIZED-EFFECTIVE POTENTIAL

Articles [C95a,C99a,CS00,HCS01]

Sometimes the limitations on present day approximate density functionals are such that it is useful to calculate an "exact" exchange-correlation potential from ab initio theory. Professor Rodney J. Bartlett has dubbed this approach "ab initio DFT". I have been one of the early contributers to the problem of including correlation in ab initio DFT [C95a,C99a]. These were important formal papers for their time.

My present aim is to develop ab initio as a tool for obtaining improved DFT orbital energies for use in applied TDDFT. We had previously shown that improving DFT orbital energies is important in the correct description of sigma excitation energies in ethylene [CS00]. Since the emphasis is ultimately on applications, we are putting a large emphasis on questions of practicality. As a first step in this direction, we have implemented Hartree-Fock (HF) calculations within the resolution-of-the-identity (RI) approximation [HCS01]. The advantage of RI-HF is that no higher than 3-center electron repulsion integrals need be evaluated. The precision is adequate for common low-resolution electronic excitation spectra.

 

 

MODELING ELECTRON MOMENTUM SPECTROSCOPY TRIPLE-DIFFERENTIAL CROSS-SECTIONS

Articles [DCSS94,C95a]

Electron momentum spectroscopy (EMS) is an (e,2e) scattering method which uses energy conservation to obtain ionization potentials and momentum conservation to measure, to a good approximation, the spherically-averaged momentum distribution of the Dyson orbital from which the electron was ionized. As the experimental resolution of EMS has improved, the spectroscopists have become eager to apply EMS to larger molecules. However, accurate calculations are required for interpreting the measured spectra. The cost of calculations using traditional ab initio methods mounts rapidly with the size of the molecule, especially since extended basis sets are required for calculating EMS cross-sections. Although the idea of using density-functional theory (DFT) for this purpose, by taking Kohn-Sham orbitals to approximate Dyson amplitudes, was heretical, my work on the optimized effective potential model showed that this idea has a rigorous meaning and is well-founded. I used a Klein-Luttinger-Ward-like energy expresssion, which is a functional of the Green function, to generalize the optimized effective potential model of the exact exchange potential in DFT to include correlation [C95a]. This made a contribution to the fundamental problem of interpreting the exchange-correlation potential, vxc, in DFT by showing that vxc is the best (in a certain variational sense) local approximation to the exchange-correlation self-energy in Dyson's quasiparticle equation. This suggested that, at least for outer valence orbitals, the Kohn-Sham orbitals might be used to approximate Dyson amplitudes. This laid the foundations for our highly successful pioneering application of DFT to calculate EMS triple differential cross-sections [DCCS94]. The ability to use DFT for this purpose has proven to be of considerable practical value for experimental EMS [see e.g. Y. Zheng, J.J. Neville, and C.E. Brion, Science 270, 786 (1995).]

SIMPLE GREEN FUNCTION SELF-ENERGY APPROXIMATIONS
 

Articles [CC89c,CC91b,HCC97]

The one-electron Green function method provides a rigorous description of ionization, electron attachment, and electron scattering processes via Dyson's quasiparticle equation. Many-body effects are included in this equation via the self-energy operator. Although sophisticated, accurate approaches to the self-energy are known, these are quite computationally demanding. Physically-motivated, simpler approximations to the self-energy are useful, both for treating larger systems and for interpretation. Little had been done to develop simple self-energy approximations that are appropriate for molecules. Hedin's GW approximation (and variants thereon) has long been used in conjunction with density-functional theory (DFT) as a state-of-the-art method for solid-state band-structure calculations but it had never been tested in the realm of quantum chemistry. Its application to chemical problems was potentially attractive since molecular Green function (GF) methods, are significantly more computationally demanding. As a first step toward the adaptation of the GW method to molecular calculations, (which were usually based on a Hartree--Fock reference state) I implemented a second-order post-Hartree-Fock treatment, and reported the first GW-type calculations on molecules [CC89c,CC91b]. These were second-order (i.e. GW2) calculations because the polarization propagator was only treated at the level of the independent particle approximation, but showed that the GW2 approximation gives ionization potentials comparable in quality to the usual second-order Green function (GF2) approximation, as long as care is taken to remove unphysical self-polarization effects in the GW2 calculation. (Although negligible in solids, these effects can result in a significant error in molecules.) This indicates that the nature of the approximations used by no means restricts the GW approximation to solids, but that it is a viable approach in the molecular realm. Although it is well-known that GF results are not particularly good at second order, my comparison of GW2 with GF2 suggests that a (self-polarization corrected) full GW calculation (i.e. using a time-dependent DFT or Hartree-Fock polarization propagator), would offer dramatically improved results while yielding significant computational advantages. In publication [HCC97], we have used the fact that the GW2 approximation already gives qualitatively correct results in order to introduce a semi-empirical scale factor leading to a GF method which is simultaneously quantitative and simple.

 

 

  • License 1 en chimie

    • CHI 110 : Structure de la Matière

      • 2003-2004 : 2 CTD

      • 2004-2005 : 2 CTD

      • 2005-2006 : 3 CTD, 1 TP

      • 2006-2007 : 3 CTD

      • 2007-2008 : 1 CTD, 1 TP

      • 2008-2009 : 1 C

      • 2009-2010 : 1C

      • 2010-2011 : 1 C, 1 CTD, 1 TP

      • 2011-2012 : 1 TP

      • 2013-2014 : 1 CTD

      • 2014-2015 : 1 CTD

      • 2015-2016 : 1 CTDTP

    • CHEM 110 Int : General Chemistry (Structure of Matter)

      • 2011-2012 : 1 C, 1 CTD

      • 2012-2013 : 1 C, 1 CTD, 2 TP

      • 2013-2014 : 1 C, 1 CTD, 1 CTDTP

      • 2014-2015 : 1C, 1 CTDTP

      • 2015-2016 : 1C, 1 CTD

    • CHI 131 : General Chemistry (Structure of Matter)

      • 2016-2017 : 1 C, 1 CTD

      • 2017-2018 : 1C, 1 CTD, 1 CTDTP

    • CHI 120 : Module Chimie Inorganique

      • 2004-2005 : C, 2 TD, 2 TP

      • 2005-2006 : C, 1 TD

      • 2006-2007 : C, 1 TD, 1 TP

      • 2007-2008 : C, 2 TD, 1 TP

      • 2008-2009 : C, 1 TD

      • 2009-2010 : C, 1 TD, 1 TP

      • 2010-2011 : C, 1 TD, 1 TP

      • 2011-2012 : C

      • 2012-2013 : C

      • 2013-2014 : C, 1 TD

      • 2014-2015 : C, 3 TD, 1 TP

      • 2015-2016 : C, 1 TP

    • CHI 120 : Module chimie organique

      • 2011-2012 : 1 TD, 1 TP

      • 2012-2013 : 1 TD

      • 2013-2014 : 1 TD, 3 TP

      • 2014-2015 : 2 CTD, 1 TP

      • 2015-2016 : 1 CTD, 1 TP

    • CHI 201 : Chimie Générale

      • 2016-2027 : 1 TD

      • 2017-2018 : 1 TD

    • CHI 231 : General Chemistry

      • 2016-2017 : 1 TD, 1 TP

      • 2017-2018 : 1 TD, 1 TP

  • License 2 en chimie

    • CHI 231

      • 2014-2015 : 1 TP

      • 2015-2016 : 1 TD, 1 TP

    • CHI 305

      • 2016-2017 : 2 TD, 2 TP

      • 2017-2018 : 2 TD

    • CHI 335

      • 2016-2017 : 1 TP

      • 2017-2018 : 1 TP

  • License 3 en chimie

    • Chimie Physique Approfondie

      • 2001-2002 : C, 1/2

      • 2002-2003 : C, 1/2 TD

      • 2003-2004 : C, 1/2 TD

      • 2008-2009 : 2/5 C, 2/5 TD

      • 2009-2010 : 2/5 C, 2/5 TD

      • 2010-2011 : 2/5 C, 2/5 TD

      • 2011-2012 : 2/5 C, 2/5 TD

      • 2012-2013 : 2/5 C, 2/5 TD

      • 2013-2014 : 2/5 C, 2/5 TD

  • License 3 Physique Chimie

    • Analyse Numérique

      • 2007-2008 : C, 3 TP

      • 2008-2009 : C, 3 TP

      • 2009-2010 : C, 3 TP

      • 2010-2011 : C, 2 TP

  • Masters 1 (M1)

  • Masters 2 (M2) en chimie physique (anciennement DEA de chimie physique)

    • Module Chimie Théorique

      • 2001-2002 : 1/2 C

      • 2002-2003 : 1/2 C

      • 2003-2004 : 1/2 C

    • TDDFT

      • Cours enseigné dans le cadre du Label National Chimie Théorique

      • 2007-2008 : 8h45 de cours

      • 2008-2009 : 10h00 de cours

      • 2010-2011 : 8h00 de cours

      • 2011-2012 : 8h00 de cours enseigné dans le cadre d'une école de nanotechnology à Rio de Janeiro (BRASSON)

      • 2012-2013 : 4h00 de cours enseigné dans le cadreu du Label à l'ENS de Lyon

    • MBPT

      • Cours enseigné dans le cadre du Label National Chimie Théorique

      • 2009-2010 : 9h00 de cours

 

 

 

Last updated: 11 November 2024

After receiving my BS in Chemistry from the University of California at Berkeley,  I went on to do my PhD in Physical Chemistry at the University of Wisconsin at Madison with Prof. John E. Harriman.  I then spent 5 years as a postdoc and research associate with Prof. Delano P. Chong at the  University of British Columbia.  This was followed by 10 years in a Senior Scientist and Computing Professional position at the University of Montreal where I was associated with the group of Prof. Dennis R. Salahub.  Since 2001 I have been professor, here in Grenoble, France, at the Grenoble Alps University (formerly the Joseph Fourier University).

I have about 80 publications and am one of the principal co-authors of the deMon codes.  According to the Web of Science, my H-index is 33 which means that I have published 33 papers with at least 33 citations each. My most cited paper has 4732 citations and I have two highly cited review articles.  I have officially directed 7 PhD theses and (before coming to Grenoble) unofficially co-directed another 4 PhD theses.

My best known work is undoubtedly in the area of time-dependent density-functional theory (TD-DFT).  Most quantum chemistry or quantum physics codes contain some implementation of my linear response formulation of TD-DFT (“Casida's equation”) which was published in the book  Recent Advances in Density-Functional Methods, Part I, edited by D. P. Chong (Singapore, World Scientific, 1995) and so is not part of the usual data base of the Web of Science.  However Google Scholar lists 1653 citations for this article.  I have been frequently called upon to give talks and summer school courses in TDDFT.

P.S. The photo on this page shows me sitting in a sculpture made by my (now deceased) mother and installed in Skjolden, Sogne og Fjordane, Norway on 23 June 2023.  Our ancestors emmigrated from this place to America around 175 years ago, but Norway remains in our traditions.   Hence it is a very special picture indeed.

 

Last updated: 9 November 2024

See also my google scholarship profile.

2020s

  1. [MDC24] D. Magero, A.M.H.M. Dargouth, and M.E. Casida, J. Photochem. Photobio. A: Chem. 451, 115502 (2024). DOI: 10.1016:j.jphotochem.2024.115502 journal link, Preprint: https://arxiv.org/abs/2311.01704.
    "Test of the Orbital-Based LI3 Index as a Predictor of the Height of the 3MLCT -> 3MC Transition-State Barrier for Gas-Phase [Ru(NˆN)3]2+
  2. [PBEC23] A. Ponra, C. Bakasa, A.J. Etindele, and M.E. Casida, J. Chem. Phys. 159, 244306 (2023). DOI: 10.1063/5.0173572 Preprint: https://arxiv.org/abs/2309.00887
    "Diagrammatic Multiplet-Sum Method (MSM) Density-Functional Theory (DFT): Investigation of the Transferability of Integrals in ``Simple'' DFT-Based Approaches to Multi-Determinantal Problems''
  3. [TANC23] W. Taouali, K. Alimi, A.S. Nangraj, and M.E. Casida, J. Comp. Chem. 44, 2130 (2023), DOI: 10.1002/jcc.27186. Preprint: https://arxiv.org/abs/2305.18085
    "Density-Functional Theory (DFT) and Time-Dependent DFT Study of the Chemical and Physical Origins of Key Photoproperties of End-Group Derivatives of the Nonfullerene Bulk Heterojunction Organic Solar Cell Acceptor Molecule IDIC"
  4. [NSK+23] Asma Sindhoo Nangraj, Saima Sipy, Abbas Khan, Gurudeeban Selvaraj, Abdulrahman Alshammari, Mark Earl Casida, and Dongqing Wei, Database 2023, 1 (2023). DOI: 10.1093/database/baad063/7303975
    "ESOMIR: a curated database of biomarker genes and miRNAs associated with esophageal cancer"
  5. [PEMC23] Abraham Ponra, Anne Justine Etindele, Ousmanou Motapon, and Mark E. Casida, Adv. Quant. Chem. 8, pages 351-372 (2023), DOI: 10.1016/bs.aiq.2023.02.004, preprint: https://arxiv.org/abs/2212.10358
    "Binding Energies for Successive Addition Reaction of .OH with C60: A Laboratory for Testing Frontier Molecular Orbital Theory"
  6. [OPEC23] Nabila B. Oozeer, Abraham Ponra, Anne Justine Etindele, and Mark Earl Casida, Pure Appl. Chem. 95, 213 (2023). https://doi.org/10.1515/pac-2022-1109, preprint: https://arxiv.org/abs/2211.16027
    "A New Freely-Downloadable Hands-on Density-Functional Theory Workbook Using a Freely-Downloadable Version of deMon2k"
  7. [MMAC22] Denis Magero, Tarek Mestiri, Kamel Alimi, and Mark E. Casida, a chapter in the book Green Chemistry and Computational Chemistry: Shared Lessons in Sustainability, edited by Liliana Mammino (Elsevier: Amsterdam, 2022), pp. 115-145. https://arxiv.org/abs/2004.03345
    ''Computational Studies of Ruthenium and Iridium Complexes for Energy Sciences and Progress on Greener Alternatives''
  8. [LC22] Latévi Max Lawson Daku and Mark Earl Casida, a chapter in the book Green Chemistry and Computational Chemistry: Shared Lessons in Sustainability, edited by Liliana Mammino (Elsevier: Amsterdam, 2022), pp. 355-384.  Preprint: https://arxiv.org/abs/1201.2398 
    "Modeling the Physical Properties of Environmentally-Friendly Optical Magnetic Switches: DFT and TD-DFT"
  9. [PEMC21] Abraham Ponra, Anne Justine Etindele, Ousmanou Motapon, and Mark E. Casida, Theo. Chem. Acc. 140, 154 (2021). DOI: 10.1007/s00214-021-02852-8. arXiv preprint, journal link
    "Practical Treatment of Singlet Oxygen with Density-Functional Theory and the Multiplet-Sum Method"
  10. [DCZ+21] Ala Aldin M. H. M. Darghouth, Mark E. Casida, Xi Zhu, Bhaarathi Natarajan, Haibin Su, Alexander Humeniuk, and Roland Mitrić, J. Chem. Phys. , 154, 054102 (2021). In the special issue on Excitons: Energetics and Spatio-temporal Dynamics https://doi.org/10.1063/5.0024559, arXiv preprint
    "Effect of Varying the TD-lc-DFTB Range-Separation Parameter on Charge and Energy Transfer in a Model Pentacene/Buckminsterfullerene Heterojunction"

2010s

  1. [TZCA19] Walid Taouali, Sami Znaidia, Mark E. Casida, and Kamel Alimi, J. Mol. Graph. Model. 89, 139 (2019). https://doi.org/10.1016/j.jmgm.2019.03.014
    ''Rational Design of (D-A) Copolymers towards High Efficiency Organic Solar Cells: DFT and TD-DFT Study''
  2. [DCJ+18] Ala Aldin M. H. M. Darghouth, Gabriela Calinao Correa, Sacha Juillard, Mark E. Casida, Alexander Humeniuk, and Roland Mitrić, J. Chem. Phys. 149, 134111 (2018); doi: 10.1063/1.5025624, arXiv preprint.
    "Davydov-Type Excitonic Effects on the Absorption Spectra of Parallel-Stacked and Herringbone Aggregates of Pentacene: Time-Dependent Density-Functional Theory and Time-Dependent Density-Functional Tight Binding"
  3. [TCDA18] W. Taouali, Mark E. Casida, Ala Aldin H. M. H. Darghouth, and K. Alimi, Comp. Mater. Sci. 150 54 (2018). DOI:10.1016/j.commatsci.2018.03.038.
    "Theoretical design of new molecules with a low band-gap for solar cell applications: DFT and TD-DFT study"
  4. [MCA+17] Denis Magero, Mark E. Casida, George Amolo, Nicholas Makau, and Lusweti Kituyi, J. Photochem. Photobiol. A, 348, 305 (2017). Preprint: https://arxiv.org/abs/1707.03665
    "Partial Density of States Ligand Field Theory (PDOS-LFT): Recovering a LFT-Like Picture and Application to Photoproperties of Ruthenium(II) Polypyridine Complexes"
  5. [TCC+17] Walid Taouali, Mark E. Casida, M. Chemek, Ayoub Haj Said, and Kamel Alimi J. Mol. Modeling 23, 41 (2017) DOI:10.1007/s00894-017-3227-x.
    "Theoretical Investigation of Oligomer Structure and Properties for [4-(Methxyphenyl)acetonitrile]n (n=1-5)"
  6. [MC17] Hemanadhan Myneni and Mark E. Casida, Comput. Phys. Comm. 213, 72 (2017) DOI:10.1016/j.cpc.2016.12.011
    "On the Calculation of Δ < S2 > for Electronic Excitations in Time-Dependent Density-Functional Theory"
  7. [DCT+15] Ala Aldin M.H.M. Darghouth, Mark E. Casida, Walid Taouali, Kamel Alimi, Mathias P. Ljungberg, Peter Koval, Daniel Sánchez-Portal, and Dietrich Foerster, Computation 3, 616 (2015). (Proceedings of the 16th International Conference on Density Functional Theory and its Applications, 31 August - 4 September 2015, Debrecen, Hungary)
    "Assessment of Density-Functional Tight-Binding Ionization Potentials and Electron Affinities of Molecules of Interest for Organic Solar Cells Against First-Principles GW Calculations"
  8. [VFC15] Omar Valsson, Claudia Filippi, and Mark E. Casida, J. Chem. Phys. 140, 144104 (2015). DOI:10.1063/1.4916354
    "Regarding the use and misuse of retinal protonated Schiff base photochemistry as a test case for time-dependent density-functional theory"
  9. [CH15] Mark E. Casida and Miquel Huix-Rotllant, Topics in Current Chemistry, special volume on Density-Functional Methods for Excited States, edited by Nicolas Ferré, Michael Filatov, and Miquel Huix-Rotllant, (Springer, 2015). DOI:10.1007/128_2015_632.
    "Many-Body Perturbation Theory (MBPT) and Time-Dependent Density-Functional Theory (TD-DFT): MBPT Insights About What is Missing in, and Corrections to, the TD-DFT Adiabatic Approximation"
  10. [WJL+14] C. Muhavini Wawire, Damien Jouvenot, Frédérique Loiseau, Pablo Baudin, Sébastien Liatard, Lydia Njenga, Geoffrey Kamau, and Mark E. Casida, J. Photochem. and Photobiol. A 276, 8 (2014). (Note that the journal has incorrectly marked 2013 instead of 2014 when they published this volume.)
    "Density-Functional Study of Lumininescence in Polypyridine Ruthenium Complexes"
  11. [NGC+12] Bhaarathi Natarajan, Luigi Genovese, Mark E. Casida, Thierry Deutsch, Olga N. Burchak, Christian Philouze, and Maxim Y. Balakirev, arXiv:1108.3475v1, Chem. Phys. 402, 29 (2012).
    "Wavelet-Based Linear-Response Time-Dependent Density-Functional Theory"
  12. [CH12] Mark E. Casida and Miquel Huix-Rotllant,  Annu. Rev. Phys. Chem. 63, 287 (2012).  DOI: 10.1146/annurev-physchem-032511-143803 Preprint:  arXiv:1108.0611v1"
    Progress in Time-Dependent Density-Functional Theory"
  13. [NCGD11] Bhaarathi Natarajan, Mark E. Casida, Luigi Genovese, Mark E. Casida, and Thierry Deutsch,
    Theoretical and Computational Methods in Modern Density Functional Theory, edited by Amlan K. Roy (Nova Science Publishers: Hauppauge, New York, USA, 2011), pp. 313-356.
    arXiv:1110.4853v1
    "Wavelets for Density-Functional Theory and Post-Density-Functional-Theory Calculations"
  14. [CND11] Mark E. Casida, Bhaarathi Natarajan, and Thierry Deutsch, http://arxiv.org/abs/1102.1849.
    in Fundamentals of Time-Dependent Density-Functional Theory, edited by Miquel Marques, Neepa Maitra, Fernando Noguiera, E.K.U. Gross, and Angel Rubio, Lecture Notes in Physics, Vol. 837 (Springer Verlag: 2011), p. 279.
    "Non-Born-Oppenheimer dynamics and conical intersections"
  15. [HIRC11] Miquel Huix-Rotllant, Andrei Ipatov, Angel Rubio, and Mark E. Casida, http://arxiv.org/abs/1101.0291, Chem. Phys., 391, 120 (2011).
    "Assessment of Dressed Time-Dependent Density-Functional Theory for the Low-Lying Valence States of 28 Organic Chromophores"
  16. [HNI+10] Miquel Huix-Rotllant, Bhaarathi Natarajan, Andrei Ipatov, C. Muhavini Wawire, Thierry Deutsch, and Mark E. Casida, Phys. Chem. Chem. Phys., 12, 12811-12825 (2010).
    "Assessment of Noncollinear Spin-Flip Tamm-Dancoff Approximation Time-Dependent Density-Functional Theory for the Photochemical Ring-Opening of Oxirane"

2000s

  1. [CCJ09] Mark E. Casida, Henry Chermette, and Denis Jacquemin, J. Mol. Struct. (Theochem) 914, 1 (2009).
    "Preface: Time-Dependent Density-Functional Theory for Molecules and Molecular Solids" (Introduction for the Theochem Special Volume on TDDFT, Guest Editors M. E. Casida, H. Chermette, and D. Jacquemin)
  2. [C09] Mark E. Casida, J. Mol. Struct. (Theochem) 914, 3 (2009).
    "Review: Time-Dependent Density-Functional Theory for Molecules and Molecular Solids"
  3. [ICJC09] Andrei Ipatov, Felipe Cordova, Loïc Joubert Doriol, and Mark E. Casida, J. Mol. Struct. (Theochem) 914, 60 (2009).
    "Excited-State Spin-Contamination in Time-Dependent Density-Functional Theory for Molecules with Open-Shell Ground States"
  4. [TTR+08] Enrico Tapavicza, Ivano Tavernelli, Ursula Rothlisberger, Claudia Filippi, and Mark E. Casida, J. Chem. Phys. 129, 124108 (2008).
    "Mixed time-dependent density-functional theory/classical surface hopping study of oxirane photochemistry"
  5. [C08] Mark E. Casida, in Computational Methods in Catalysis and Materials Science, part of the IDECAT Course book series, Philippe Sautet and Rutger A. van Santen, editors (Wiley-VCH: Weinheim, Germany, 2008), ISBN 978-3-527-32032-5, pp. 33-59.
    "TDDFT for Excited States"
  6. [CJI+07] Felipe Cordova, L. Joubert Doriol, Andrei Ipatov, Mark E. Casida, Claudia Filippi, and Alberto Vela, arXiv:0708.1381v1 [cond-mat.other] 10 Aug 2007, J. Chem. Phys. 127, 164111 (2007).
    "Troubleshooting Time-Dependent Density-Functional Theory for Photochemical Applications: Oxirane"
  7. [ZBF+07] Samir Zein, Serguei A. Borshch, Paul Fleurat-Lessard, Mark E. Casida, and Henry Chermette, J. Chem. Phys. 126, 014105 (2007).
    "Assessment of the exchange-correlation functionals for the physical description of spin transition phenomena by DFT methods: All the same?"
  8. [CIC06] M.E. Casida, A. Ipatov, and F. Cordova, in Time-Dependent Density-Functional Theory, edited by M.A.L. Marques, C. Ullrich, F. Nogueira, A. Rubio, and E.K.U. Gross, Lecture Notes in Physics (Springer: Berlin, 2006), pp. 243-257.
    "Linear-Response Time-Dependent Density-Functional Theory for Open-Shell Molecules"
  9. [IFP+06] Andrei Ipatov, Antony Fouqueau, Carlos Perez del Valle, Felipe Cordova, Mark E. Casida, Andreas M. Köster, Alberto Vela, and Christine Jödicke Jamorski, J. Molec. Struct. (Theochem) 762, 179 (2006).
    ''Excitation Energies from an Auxiliary-Function Formulation of Time-Dependent Density-Functional Response Theory with Charge Conservation Constraint''
  10. [LVH+05] Latévi Max Lawson Daku, Alfredo Vargas, Andreas Hauser, Antony Fouqueau, and Mark E. Casida, ChemPhysChem 6, 1393 (2005).
    ''Assessment of Density Functionals for the High-Spin/Low-Spin Energy Difference in the Low-Spin Iron(II) Tris(2,2'-bipyridine) Complex"
  11. [GBF+05] Georg Ganzenmüller, Nabil Berkaïne, Antony Fouqueau, Mark E. Casida, and Markus Reiher, J. Chem. Phys. 122, 234321 (2005).
    "Comparison of Density Functionals for Differences Between the High (5T2g) and Low (1A1g) Spin States of Iron(II) Coordination Compounds: IV. Results for the Ferrous Complexes [Fe(L)('NHS4')]"
  12. [FCL+05] Antony Fouqueau, Mark E. Casida, Latevi Max Lawson Daku, Andreas Hauser, and Frank Neese, J. Chem. Phys. 122, 044110 (2005)
    "Comparison of Density Functionals for Energy and Structural Differences Between the High [5T2g: (t2g)4(eg)2] and Low [1A1g: (t2g)6(eg)0] Spin States of Iron(II) Coordination Compounds: II. More Functionals and the Hexaminoferrous Cation, [Fe(NH3)6]2+"
  13. [C05] Mark E. Casida, J. Chem. Phys. 122, 054111 (2005).
    "Propagator Corrections to Adiabatic Time-Dependent Density-Functional Theory Linear Response Theory"
  14. [FMC+04] Antony Fouqueau, Sébastien Mer, Mark E. Casida, Latevi Max Lawson Daku, Andreas Hauser, Tsonka Mineva, and Frank Neese, J. Chem. Phys. 120, 9473 (2004).
    "Comparison of Density Functionals for Energy and Structural Differences Between the High [5T2g: (t2g)4(eg)2] and Low [1A1g: (t2g)6(eg)0] Spin States of the Hexaquoferrous Cation, [Fe(H2O)6]2+"
  15. [JC04] Christine Jödicke Jamorski and Mark E. Casida, J. Phys. Chem. B 108, 7132-7141 (2004).
    "Time-Dependent Density Functional Theory Investigation of the Fluorescence Behavior as a Function of Alkyl Chain Size for the 4-(N,N-Dimethylamino)benzonitrile-like Donor-Acceptor Systems 4-(N,N-Diethylamino)benzonitrile and 4-(N,N-Diisoipropylamino)benzonitrile"
  16. [FCS03] Elisa Fadda, Mark E. Casida, and Dennis R. Salahub, J. Phys. Chem. A 107, 9924 (2003).
    "14,15N NMR Shielding Constants from Density-Functional Theory"
  17. [CW04] M.E. Casida and T.A. Wesolowski, Int. J. Quant. Chem. 96, 577 (2004).
    "Generalization of the Kohn-Sham Equations with Constrained Electron Density (KSCED) Formalism and its Time-Dependent Response Theory Formulation"
  18. [FCS03b] E. Fadda, M.E. Casida, and D.R. Salahub, J. Chem. Phys. 118, 6758 (2003).
    "NMR Shieldings from Sum-Over-States Density-Functional Theory: Further Testing of the 'Loc.3' Approximation"
  19. [FCS03a] E. Fadda, M.E. Casida, and D.R. Salahub, Int. J. Quant. Chem. 91, 67 (2003).
    "Time-Dependent Density-Functional Theory as a Foundation for a Firmer Understanding of Sum-Over-States Density-Functional-Perturbation Theory: The 'Loc.3' Approximation"
  20. [HCS02] S. Hamel, M.E. Casida, and D.R. Salahub, J. Chem. Phys. 116, 8276 (2002).
    "Exchange-only optimized effective potential for molecules from resolution-of-the-identity techniques: Comparison with the local density approximation, with and without asymptotic correction"
  21. [HDCS02] S. Hamel, P. Duffy, M.E. Casida, and D.R. Salahub, J. Electr. Spectr. and Related Phenomena 123, 345 (2002).
    "Kohn-Sham Orbitals and Orbital Energies: Fictitious Constructs but Good Approximations All the Same"
  22. [C01] M.E. Casida, in Accurate Description of Low-Lying Molecular States and Potential Energy Surfaces, ACS Symposium Series 828, edited by Mark R. Hoffmann and Kenneth G. Dyall (ACS Press: Washington, D.C., 2002), ISBN 0-8412-3792-1, (Proceedings of ACS Symposium, San Diego, Calif., 2001), pp. 199-220.
    "Jacob's ladder for time-dependent density-functional theory: Some rungs on the way to photochemical heaven"

  23. [VCSC01] I. Vedernikova, M. Claeys, D.R. Salahub, and M.E. Casida, Int. J. Mass Spectroscopy 210/211, 21 (2001).
    "Excitation processes in alkali-cationized esters: A molecular orbital study"
  24. [HCS01] Sébastien Hamel, Mark E. Casida, and Dennis R. Salahub, J. Chem. Phys. 114, 7342 (2001).
    "Assessment of the quality of orbital energies in resolution-of-the-identity Hartree-Fock calculations using deMon auxiliary basis sets"
  25. [CS00] Mark E. Casida and Dennis Salahub, J. Chem. Phys. 113, 8918 (2000).
    "Asymptotic correction approach to improving approximate exchange-correlation potentials: Time-dependent density-functional theory calculations of molecular excitation spectra"
  26. [CGG+00] Mark E. Casida, Fabien Gutierrez, Jingang Guan, Florent-Xavier Gadea, Dennis Salahub, and Jean-Pierre Daudey, J. Chem. Phys. 113, 7062 (2000).
    "Charge-transfer correction for improved time-dependent local density approximation excited-state potential energy curves: Analysis within the two-level model with illustration for H2 and LiH"
  27. [GCS00] J. Guan, M.E. Casida, and D.R. Salahub, J. Molec. Structure (Theochem), 527, 229 (2000).
    "Time-dependent density-functional theory investigation of excitation spectra of open-shell molecules"

1990s

  1. [C99b] M.E. Casida, in the On-line Workshop Proceedings of the Joint ITP/INT Workshop on Time-Dependent Density Functional Theory,
    15-17 April 1999, Institute for Theoretical Physics, University of California at Santa Barbara: http://online.itp.ucsb.edu/online/tddft_c99/
    "Reconciling of the DeltaSCF and TDDFT Approaches to Excitation Energies in DFT: A Charge-Transfer Correction for TDDFT with GGA Functionals"
  2. [C99a] M.E. Casida, Phys. Rev. B 59, 4694 (1999).
    "Correlated optimized effective potential treatment of the derivative discontinuity and of the highest occupied Kohn-Sham eigenvalue: A Janak-type theorem for the optimized effective potential method"
  3. [CCS98] M.E. Casida, K.C. Casida, and D.R. Salahub, Int. J. Quant. Chem. 70, 933 (1998). (International Journal of Quantum Chemistry, Quantum Chemistry Symposium No. 32, Proceedings of the International Symposium on Atomic, Molecular, and Condensed Matter Theory)
    "Excited-state potential energy curves from time-dependent density-functional theory: A cross-section of formaldehyde's 1A1 manifold"
  4. [CJCS98] M.E. Casida, C. Jamorski, K.C. Casida, and D.R. Salahub, J. Chem. Phys. 108, 4439 (1998).
    "Molecular excitation energies to high-lying bound states from time-dependent density-functional response theory: Characterization and correction of the time-dependent local density approximation ionization threshold"
  5. [HCC97] C.-H. Hu, D.P. Chong, and M.E. Casida, J. Electron Spectr. 85, 39 (1997).
    "The parameterized second-order Green function times screened interaction (pGW2) approximation for calculation of outer valence ionization potentials"
  6. [C96] M.E. Casida, in Recent Developments and Applications of Modern Density Functional Theory, edited by J.M. Seminario (Elsevier, Amsterdam, 1996), p. 391.
    "Time-Dependent Density Functional Response Theory of Molecular Systems: Theory, Computational Methods, and Functionals"
  7. [JCS96] Christine Jamorski, Mark E. Casida, and Dennis R. Salahub, J. Chem. Phys. 104, 5134 (1996).
    "Dynamic Polarizabilities and Excitation Spectra from a Molecular Implementation of Time-Dependent Density-Functional Response Theory: N2 as a Case Study"
  8. [GCKS95] Jingang Guan, Mark E. Casida, Andreas M. Koester, and Dennis R. Salahub, Phys. Rev. B 52, 2184 (1995).
    "All-Electron Local and Gradient-Corrected Density-Functional Calculations of Nan Dipole Polarizabilities for n=1-6"
  9. [C95b] M.E. Casida, in Recent Advances in Density Functional Methods, Part I, edited by D.P. Chong (Singapore, World Scientific, 1995), p. 155.
    "Time-dependent density-functional response theory for molecules''
  10. [C95a] Mark E. Casida, Phys. Rev. A 51, 2005 (1995).
    "Generalization of the Optimized Effective Potential Model to Include Electron Correlation: A Variational Derivation of the Sham--Schluter Equation for the Exact Exchange-Correlation Potential''
  11. [CJB+94] M.E. Casida, C. Jamorski, F. Bohr, J. Guan, and D.R. Salahub, in Theoretical and Computational Modeling of NLO and Electronic Materials, edited by S.P. Karna and A.T. Yeates (ACS Press: Washington, D.C., 1996), (Proceedings of ACS Symposium, Washington, D.C., 1994), p. 145.
    "Optical Properties from Density-Functional Theory"
  12. [DCCS94] Patrick Duffy, Delano Chong, Mark E. Casida, and Dennis R. Salahub, Phys. Rev. A 50, 4707 (1994).
    "Assessment of Kohn--Sham Density-Functional Orbitals as Approximate Dyson Orbitals for the Calculation of Electron-Momentum-Spectroscopy Scattering Cross Sections''
  13. [MMCS94] Vladimir G. Malkin, Olga L. Malkina, Mark E. Casida, and Dennis R. Salahub, J. Am. Chem. Soc. 94, 5898 (1994).
    "NMR Shielding Tensors Calculated with a Sum-Over-States Density Functional Perturbation Theory (SOS-DFPT)''
  14. [GDC+93] Jingang Guan, Patrick Duffy, Jonathan T. Carter, Delano P. Chong, Kim C. Casida, Mark E. Casida, and Michael Wrinn, J. Chem. Phys. 98, 4753 (1993).
    "Comparison of Local-Density and Hartree-Fock Calculations of Molecular Polarizabilities and Hyperpolarizabilities''
  15. [HC93] John E. Harriman and Mark E. Casida, Int. J. Quant. Chem. 45, 263 (1993).
    "Husimi Representation for Stationary States"
  16. [DCB+92] Patrick Duffy, S.A.C. Clark, C.E. Brion, Mark E. Casida, D.P. Chong, E.R. Davidson, and C. Maxwell, Chem. Phys. 165, 183 (1992).
    "Electron Momentum Spectroscopy of the Valence Orbitals of Acetylene: Quantitative Comparisons Using Near Hartree-Fock Limit and Correlated Wavefunctions"
  17. [DCBC92] P. Duffy, M.E. Casida, C.E. Brion, and D.P. Chong, Chem. Phys. 159, 347 (1992).
    "Assessment of Gaussian-Weighted Angular Resolution Functions in the Comparison of Quantum Mechanically Calculated Electron Momentum Distributions with Experiment"
  18. [CC91b] Mark E. Casida and Delano P. Chong, Phys. Rev. A 44, 5773 (1991).
    "Simplified Green-function approximations: Further assessment of a polarization model for second-order calculation of outer-valence ionization potentials in molecules"
  19. [CC91a] Mark E. Casida and Delano P. Chong, Int. J. Quant. Chem. 40, 225 (1991).
    "Quasi-Particle Equation from the Configuration-Interaction (CI) Wave-Function Method"

1980s

  1. [CC89c] Mark E. Casida and Delano P. Chong, Phys. Rev. A 40, 4837 (1989); Erratum, ibid 44, 6151 (1991).
    "Physical interpretation and assessment of of the Coulomb-hole and screened-exchange approximation for molecules"
  2. [CC89b] Mark E. Casida and Delano P. Chong, Chem. Phys. 133, 47 (1989); Erratum, ibid 136, 489 (1989).
    "Contribution of correlation and relaxation to generalized overlaps for outer-valence ionization"
  3. [CC89a] Mark E. Casida and Delano P. Chong, Chem. Phys. 132, 391 (1989).
    "Large r approximation for spherically averaged momentum distributions"
  4. [C88] Mark E. Casida, Int. J. Quant. Chem. 33, 53 (1988).
    "Use of Invariants in Bounding 2-Fermion Reduced Density Matrix Eigenvalues"
  5. [CHA87] Mark E. Casida, John E. Harriman, and James L. Anchell, Int. J. Quant. Chem. S21, 435 (1987).
    "The Husimi Function for Electron Distributions"
  6. [CC89c] Mark E. Casida and Delano P. Chong, Phys. Rev. A 40, 4837 (1989); Erratum, ibid 44, 6151 (1991).
    "Physical interpretation and assessment of of the Coulomb-hole and screened-exchange approximation for molecules"
  7. [CC89b] Mark E. Casida and Delano P. Chong, Chem. Phys. 133, 47 (1989); Erratum, ibid 136, 489 (1989).
    "Contribution of correlation and relaxation to generalized overlaps for outer-valence ionization"
  8. [CC89a] Mark E. Casida and Delano P. Chong, Chem. Phys. 132, 391 (1989).
    "Large r approximation for spherically averaged momentum distributions"
  9. [C88] Mark E. Casida, Int. J. Quant. Chem. 33, 53 (1988).
    "Use of Invariants in Bounding 2-Fermion Reduced Density Matrix Eigenvalues"
  10. [CHA87] Mark E. Casida, John E. Harriman, and James L. Anchell, Int. J. Quant. Chem. S21, 435 (1987).
    "The Husimi Function for Electron Distributions"

1970s

  1. [TCBS79] Michael Trenary, Mark E. Casida, Bernard R. Brooks, and Henry F. Schaefer III, J. Am. Chem. Soc. 101, 1638 (1979).
    "Three Isomers of the Al-C2H2 System''

Publié le 8 novembre 2024

Mis à jour le 12 novembre 2024